A paper of mine just came out in Journal of the Atmospheric Sciences (JAS)! I love the feeling of seeing a paper finally come out.
Hannah, W. M., B. E. Mapes, and G. S. Elsaesser, 2016: A Lagrangian View of Moisture Dynamics During DYNAMO. J. Atmos. Sci., 73, 1967-1985.
I really liked doing this work, although it’s not exactly ground breaking. The main message of the paper is similar to countless papers in that we argue that a bottom-heavy heating profile (i.e. shallow convection; see dashed line in figure below) is important for a Tropical air mass to transition to a “very wet” state.

Although this conclusion is not new, I like the approach we used to show this. It all revolves around a pseudo-Lagrangian tendency of a column of air. In reality, we cannot “track” entire columns of air (hence the “pseudo” part), but we can estimate the instantaneous tendency as if we were following it. The trick is to write the column integrated moisture budget with horizontal advection on the left-hand side, and vertical advection, precipitation and evaporation on the right.
![]()
In this case, the things on the left can be estimated from observations with some confidence, but the things on the right are much harder to constrain. So why bother measuring the stuff on the right? Why not just lump them all together and just calculate the stuff on the left?
![]()
This leaves the lump of stuff on the right as the residual. I refer to the stuff on the left as the Lagrangian column water vapor tendency (LCT).
This is very useful for field observations, however, one of our main conclusions is that the sounding array during DYNAMO is ineffective at measuring horizontal moisture advection! So estimating the LCT from these observations can actually be very misleading. The two plots below show the column water vapor (CWV) field from 00Z on October 1, 2011 from the DYNAMO large-scale sounding array (LSA) and satellite data (MIMIC). You can see how the LSA misses the patch of dry air in the middle of the northern array. This leads to a pretty big error in the moisture advection.
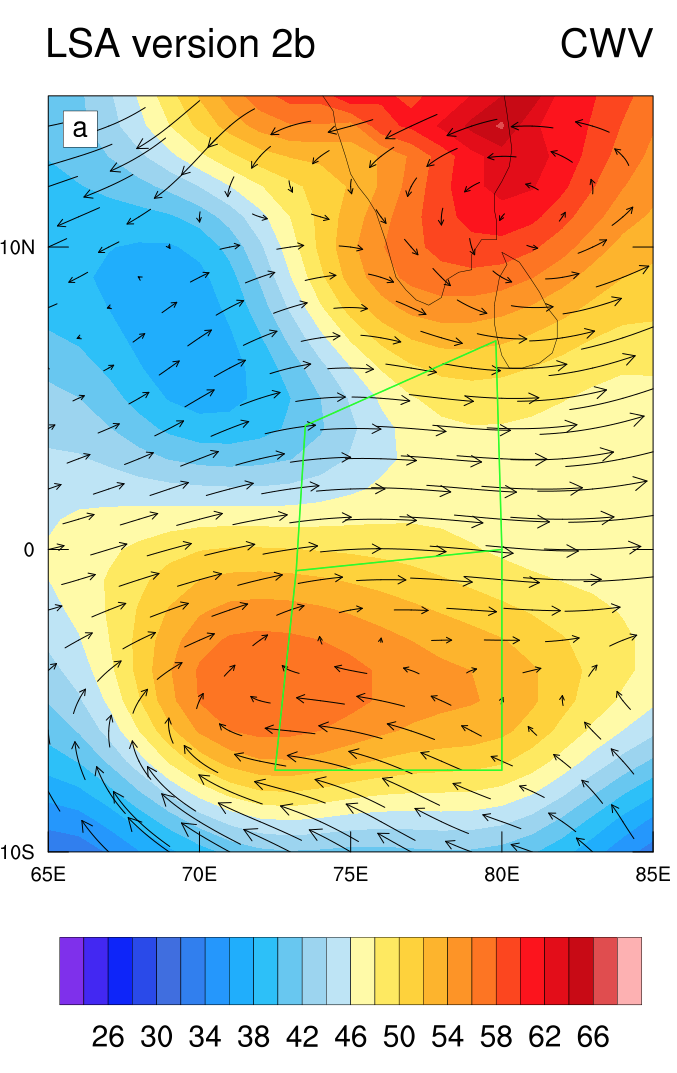
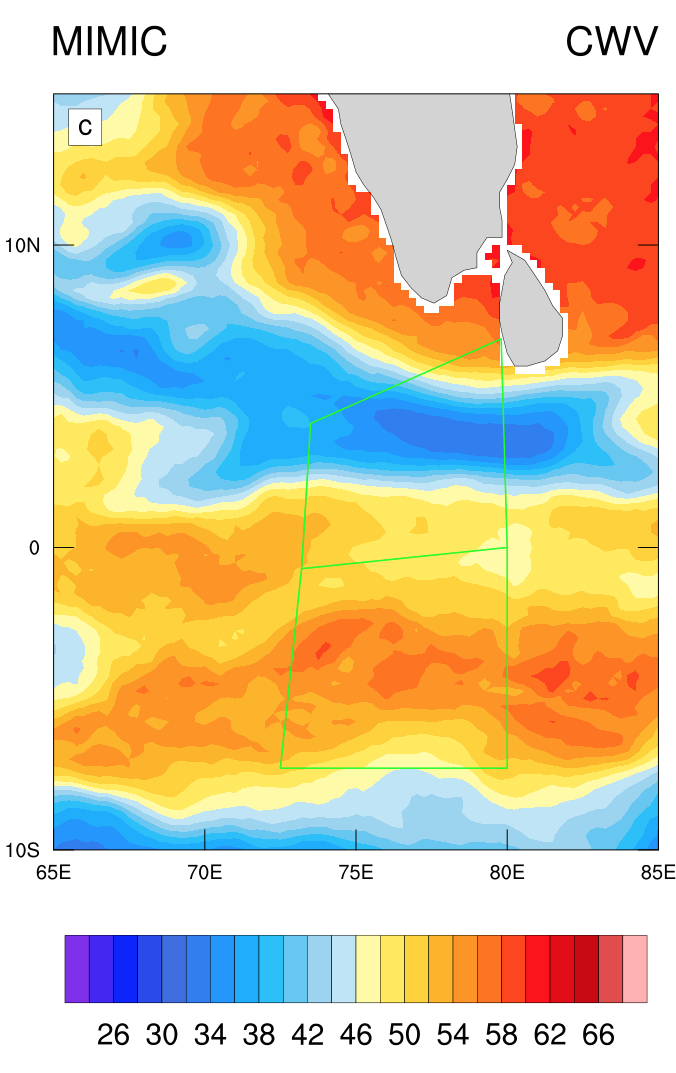
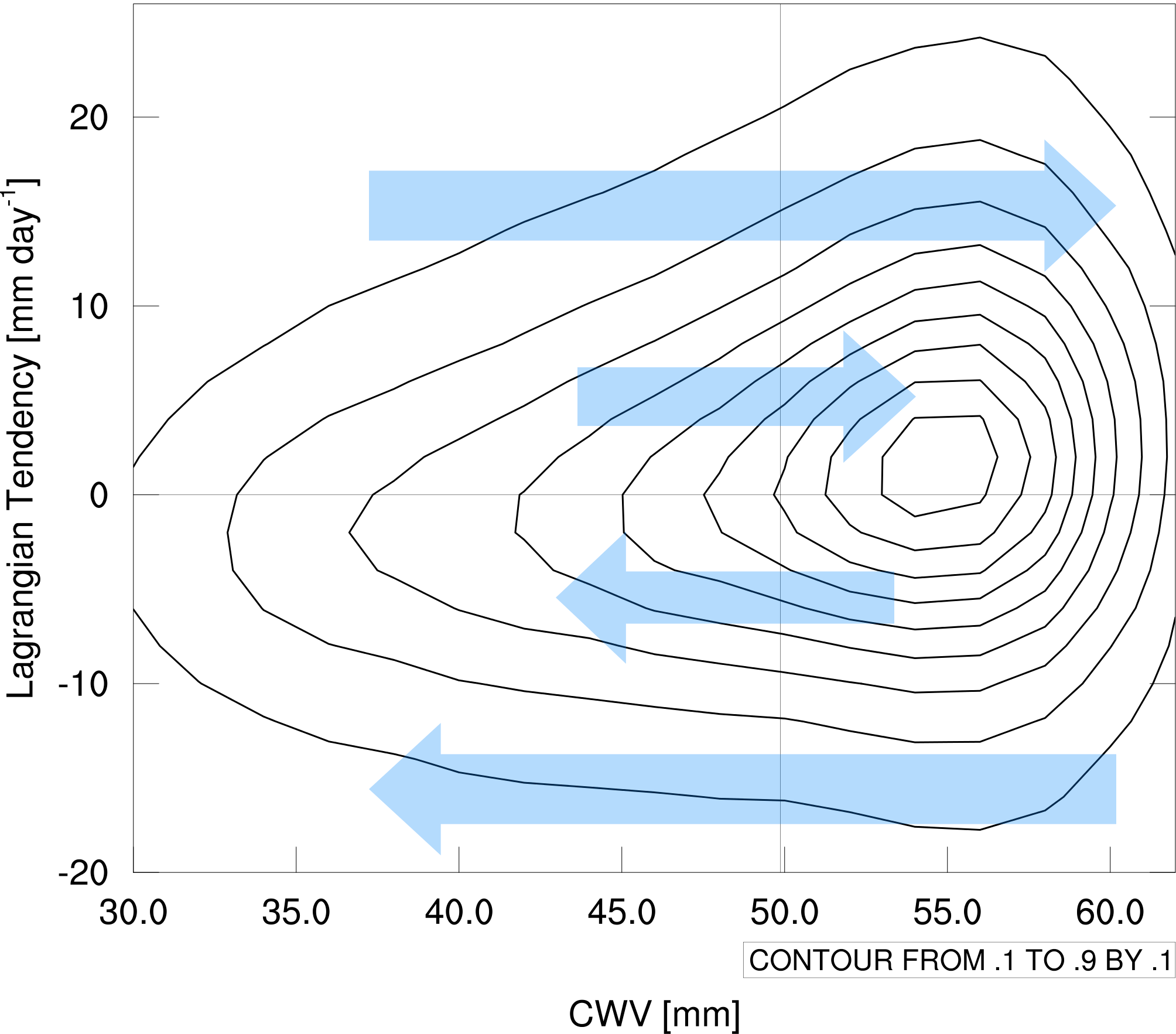
The most interesting thing about the LCT is that you can make a “phase space” with LCT and CWV (see below). The LCT is basically the tendency along the CWV axis, so a column at any point on this phase space will be push right or left depending on the value of the LCT (blue arrows). The contours show the frequency of occurrence in the phase space.
So now if we make a simple index for when the heating profile matches a bottom-heavy profile (dashed line in the first plot), we can plot this index against the phase space to see what conditions shallow convection is associated with.
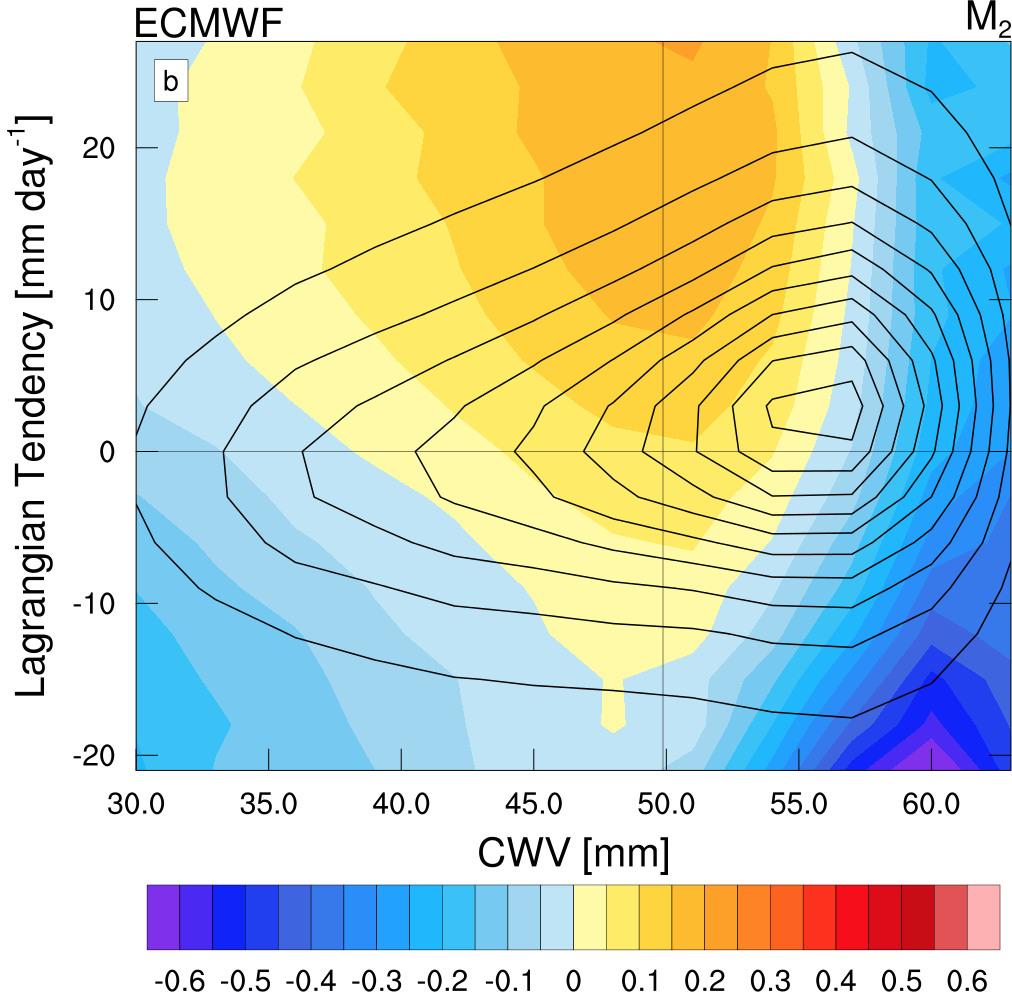
And as we expect, shallow convective heating tends to occur when the LCT is positive, which implies that shallow convection plays a role in increasing the moisture of an air mass. Interestingly, this also tends to occur near 50 mm of CWV, which is where there is a rapid transition between light and heavy rain rates (Bretherton et al. 2004; Neelin et al. 2009).

Nice walter….Congrats……pls upload full paper, what is your e-mail id ….
Thanks Abhi, I’ll email it to you.
Congrats!
Thanks!